2013年に量子コンピューティングのための関数型プログラミング言語Quipperが発表されました(Quipper: A Scalable Quantum Programming Language - arXiv、以下Quipperレポート)。QuipperはHaskell言語内のDSLとして作成された言語で、もともとは IARPA Quantum Computer Science (QCS) Programのなかで開発されたものであり、とてもよく考えられた言語です。Google Scholarでみても被引用数が444(2023年2月時点)あり、量子プログラミング言語のひとつの参照点になっているものだと思います。
ということで、今回はこのQuipperレポートをもとに量子プログラミングについてみていきたいと思います。
量子コンピューターとは
現在のところ、実用的な量子コンピューターはQRAM(Quantum Random Access Machine)モデルの形をとると考えられています。このモデルでは、量子コンピューターは古典コンピューターに接続された特殊なデバイスでコプロセッサのように動作するものと想定されます。デバイスにはアドレス指定可能なn個の量子ビットがあり、実行できる命令は、
- ユニタリー操作、たとえばk番目の量子ビットに組込みの量子ゲートUを適用する、など
- 測定、たとえばk番目の量子ビットを測定して、0または1のいずれかを返す、など
- 初期化、たとえばk番目の量子ビットを0にリセットする、など
の3つだけです。プログラムの制御フローはあくまで古典的なもので、一部の計算だけが量子デバイス上で行われて結果が戻されるということです。そして結果をもとに古典デバイスでさらに計算を行い、量子アルゴリズムのパラメーターを調整して、再度量子デバイスに仕掛ける、という具合です。
QRAMモデルは理想モデルであり、実際の量子コンピューターでは物理的な制約が課されます。量子状態の安定時間が短いのでゲートをたくさん適用できないとか、量子誤り訂正をいれなければならない、とかです。あるいはQRAMモデルではユニタリー操作を1つずつ適用する想定ですが、処理時間を短くするために多数のゲートを事前に計算しておいて一括適用する(回路モデル)というのもあります。
量子プログラミング言語に求められるもの
そうすると量子コンピューター上のプログラミングとは単にユニタリー操作や測定を組み合わせて順番に適用するだけという話になりますが、実はそう単純ではありません。というのも、量子コンピューターには量子力学的な制約が課されるため、量子プログラミングは古典的なものとはやや異なるものになるからです。
量子情報にまつわる禁止定理はいくつかありますが(たとえばQuantum information - Wikipediaを参照)、一例として特に有名な複製不可能定理(No-cloning theorem)があります。これは未知の量子状態をコピーすることはできないというもので、プログラミングにも直接的に影響を及ぼします。たとえばQuipperでは次のようなコードを書くことができますが、
bad :: Qubit -> Circ Qubit bad a = qnot a `controlled` a -- aが2回使われている!
コードのユニタリー操作中で量子ビットaが2回使われており、これを実行するにはaの状態を別の量子ビットにコピーしておいてからユニタリー操作を適用することになりますが、そのコピーが複製不可能定理に反するため、このような操作は量子力学的に不可能ということになります。こんな具合で、量子コンピューター上のプログラミングは古典とはやや異なるものになります。
それでは量子プログラミング言語にはどのような機能が求められるのか?ということですが、Quipperレポートの内容を簡単にまとめると、次のように述べられています。
まずはハードウェア非依存であることです。上述の通り実際の量子コンピューターでは様々な物理的なハードウェア制約が課されますが、プログラミング言語のデザインとしてはそのようなハードウェアの詳細は抽象化して、プログラマーに対しては統一された計算モデルとしてみせたほうがよいとしています。
Quipperではコンパイル時、回路生成時、回路実行時の3つの実行段階に分けることでハードウェアの詳細を吸収しています。またこれによって回路を実機ではなくシミュレーターで走らせたり、回路図を描画したりする機能もサポートしています。
もうひとつは、できるだけアルゴリズム設計者の意図に近いレベルの抽象度で量子アルゴリズムを書けるべきである、ということです。例として量子アルゴリズムでよくあるテクニックを5つ紹介しています。
1つめは量子アルゴリズムでよく使われるテクニックのサポートです。量子フーリエ変換や振幅増幅、量子ウォークなどのテクニックは古典コンピューターの性能を上回るための量子アルゴリズムの核としてよく使われますので、これらに対して特別はサポートがあったほうがよいということだと思います。
2つめはオラクルのサポートです。オラクルとは実装に興味のない補助関数のようなもので、ここでは問題の入力を与える関数などのことを指し、グラフの辺、ゲームの勝敗などの記述に利用されます。オラクル実装が面倒なのは想像できますが、さらに量子オラクルとなると通常は次の4ステップを踏むそうでより面倒です:
- オラクルを古典的なプログラムとして作成する
- プログラムを入力サイズに応じた古典回路に変換する
- 古典回路を量子回路に変換する
- 最後に量子回路を可逆にする。
を
に置き換える
最後のステップは逆演算(uncomputation)というよく使われるテクニックで、回路を可逆にしつつ使い終わった補助量子ビットを初期化して戻すというものです。Quipperでは1より後のステップを自動生成する機能があるそうです。
また補助量子ビットはアルゴリズムを組むときには大抵必要になりますが、今どの量子が空いているかなどをプログラマーが意識するのは大変です。Quipperでは補助量子ビットの管理もサポートしています。
3つめは回路ファミリーのサポートです。ほとんどの量子アルゴリズムは入力サイズなどのパラメーターを持っており、1つの回路というよりもパラメタライズされた回路ファミリーとなります。
4つめは回路操作です。量子アルゴリズムが最終的にはゲートと測定の組み合わせに分解されると言っても、アルゴリズムを記述する上では意味ある回路単位で記述できるほうがよいとしています。
5つめは古典言語と量子言語はできるだけシームレスにあるべきということです。QRAMモデルでは計算が古典と量子の間を行き来します。なので量子プログラミング言語では古典と量子の両方を記述できる必要があります。しかし上述のように量子プログラミングでは量子力学からの強い制約があるため、古典と量子では明確な区別も必要になります。QuipperではHaskellで柔軟に型付けをして対応しています。
線形型と依存型による改良
すでに触れましたが、Quipperでは複製不可能定理に反するコードが書けてしまうという問題がありました。
bad :: Qubit -> Circ Qubit bad a = qnot a `controlled` a -- aが2回使われている!
これはQuipperレポート内でも課題として取り上げられており、より多くのエラーをコンパイル時に検知するには線形型や依存型が必要だ、と述べられています。現在では複製不可能定理を強制するには線形型を利用できることが知られていますし、パラメタライズされた回路は依存型を使って表現することもできます。HaskellにもGHC拡張として LinearTypes や DataKinds がありますが、Quipper作成中の頃はまだリリースされていませんでした。
Quipperの発表後、Quipperに対して線形型や依存型を追加した改良版がProto-QuipperやLinear-Quipperなどいくつか提案されていますが、その中でもここではQimaeraというIdris2の言語内DSLとして実装された量子プログラミング言語をもとに、線形型と依存型の利用方法を少しだけ見ていきたいと思います(Qimaera: Type-safe (Variational) Quantum Programming in Idris - arXiv)。
ところで線形型と依存型の両方を持つというのはどうも簡単ではないらしいのですが(Conor McBrideによると「意図的かつ成功裏に回避されてきた」らしいですが…)、そのMcBrideのアイディアをもとに2018年にQuantitative Type Theory(日本語訳が分かりませんが量的型理論でしょうか、以下QTT)が作られました(The Syntax and Semantics of Quantitative Type Theory - BOB ATKEY)。QTTは依存型であるMartin-Löfの型理論をベースに、変数が使われる回数を正確に管理することで依存型に線形型も統合した型理論になっています。そしてIdrisの作者が2020年頃からQTTをコアとして新しく実装しなおしたIdris2を開発しており、QTTを実際にプログラミング言語として試すことができます。QimaeraはIdris2の線形型や依存型の機能を活用して作成されています。
さてQimaera論文からの例ですが、下のようなコードがあったとします(見た目がHaskellに似てますがIdris2のコードです):
toBellBasis : Unitary 2 toBellBasis = CNOT 0 1 (H 0 IdGate )
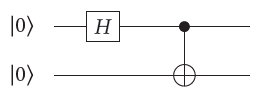
2つの量子ビットがあり、まず0番目の量子にHadamardゲートを適用して、そのあと0と1番目にControlled-Notゲートを適用することでベル状態を作る、というコードです。このとき間違えて CNOT 1 1と書いてしまったらどうなるか考えます。そもそも同じ量子にCNOTを適用するというのは物理的に意味をなさないわけですが、Qimaeraでは次のようなコンパイルエラーになります:
Error: While processing right hand side of
toBellBasis. Can't find an implementation fornot (equalNat 1 1) = True.
下にCNOTの定義を一部抜粋しましたが、CNOTは引数の数字が異なることの証明(prf3 : (c /= t) = True)を要求しているため、そこが通らなかったのでエラーになったと分かります。これは依存型でチェックする例です。
data Unitary : Nat -> Type where IdGate : .... -- 省略 H : .... -- 省略 P : .... -- 省略 CNOT : (c : Nat) -> (t : Nat) -> {auto prf1 : (c < n) = True} -> {auto prf2 : (t < n) = True} -> {auto prf3 : (c /= t) = True} -- ここの証明でエラーになっている -> Unitary n -> Unitary n
次もQimaera公式の例(Qimaera/ExampleDetectableErrors.idr - GitHub)からですが、次のコードでは量子ビットを表わすq4変数を2回利用したせいでコンパイルエラーになります:
-- In this example, we try to copy a qubit brokenOp2 : IO (Vect 5 Bool) brokenOp2 = run (do [q1,q2,q3,q4] <- newQubits {t = SimulatedOp} 4 [b3] <- measure [q3] [q4,q1,q5] <- applyUnitary [q4,q1,q4] (X 0 IdGate) --trying to copy q4 [b1,b2,b5] <- measure [q1,q2,q5] pure [b1,b2,b3,b5,b5] )
Error: While processing right hand side of
brokenOp2. There are 2 uses of linear nameq4.
コメントの個所(applyUnitary [q4,q1,q4] (X 0 IdGate))でq4変数が2回使われており、このような操作は(先に触れたように)複製不可能定理に反するのですが、線形型のチェックによってコンパイルエラーとして検知されています。
このように線形型や依存型は量子プログラミングを安全にするためにとても役に立つものだと分かります。ただ既存の量子プログラミング言語で有名なものは、Quipperを含めて、IBMのQiskit、MicrosoftのQ#、GoogleのCirqなど、いずれも線形型、依存型をサポートしていません。なのでこれらの型理論がメジャーになっていくのかどうかは分かりませんが、量子プログラミングによって注目を集めるというのは面白いことだなと思います。
採用情報
朝日ネットでは新卒採用・キャリア採用を行っております。


