開発部のgedokuです。
HaskellをeDSLのホスト言語として使うことの魅力を、作図を通じて伝えるシリーズの第二弾です。
第一弾はこちら。
前置き
今回は円筒を描くことに主眼をおいた記事になります。
ただし、その前に第一弾の「目標図」にある、角に丸みのある長方形を描くという課題に触れたいと思います。

角に丸みをつける
目標図に描かれているサーバーのノードは、角に丸みのある長方形をしていますが、第一弾では角張った長方形しか描きませんでした。
第一弾の最後の、テキストを図形で囲む関数という例に基づいて、 今回は丸みを帯びた長方形がテキストを囲んだ図を作りましょう。
myDiagram :: Diagram B myDiagram = dia1 ||| strutX 2 ||| dia2 where dia1 = fc lightgreen $ getDiaForText "Some very very very very long text" dia2 = fc lightskyblue $ getDiaForText "a" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape = undefined
前回のmkShapeの定義では、diagramsのrectという角張った長方形を表現する関数を使用しましたが、
今回はdiagramsの提供している別の関数を使います。
roundedRect :: (InSpace V2 n t, TrailLike t, RealFloat n) => n -> n -> n -> t
rectに似ていますが、その3つ目の引数が相違点です。
それは各角の半径を指定する引数です。
myDiagram :: Diagram B myDiagram = dia1 ||| strutX 2 ||| dia2 where dia1 = fc lightgreen $ getDiaForText "Some very very very very long text" dia2 = fc lightskyblue $ getDiaForText "a" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape w h = roundedRect w h radius radius = 0.5

textShapeSimpleの図形を作る引数は次のような型を持っています:Double -> Double -> Diagram B。
そして、1つ目の引数は幅、2つ目は高さです。
もしroundedRectの引数の順が:半径、幅、高さという順であれば、半径の設定をするだけで出来たのですが、
実は半径は3つめの引数になっているため、mkShapeの定義で引数を適当に移し替える必要
があります。引数の順番を変えてからtextShapeSimpleに渡せる形になりました。
完全を期すために一部の角だけ丸みを帯びる、または角ごとに別の半径を指定出来る関数も紹介します。
roundedRect' :: (InSpace V2 n t, TrailLike t, RealFloat n) => n -> n -> RoundedRectOpts n -> t
RoundedRectOptsという引数の扱い方は一見不明ですが、その定義を参照することで明らかになります:
data RoundedRectOpts d = RoundedRectOpts { _radiusTL :: d , _radiusTR :: d , _radiusBL :: d , _radiusBR :: d }
単に4つのメンバーの組み合わせです。
dはどの型を受けてもいいとしても、roundedRect'に適用するにはRealFloatというtypeclassのインスタンス
にしなければならないので、Doubleにします。
roundedRect'を使用する際の設定の基盤としてRoundedRectOptsのDefaultインスタンスが備わっています。
インスタンスの実装は、各角の半径が0となります。すなわち丸みがない長方形ということです。
instance (Num d) => Default (RoundedRectOpts d) where def = RoundedRectOpts 0 0 0 0
もう一つ備わっているのは、各設定対象へのlensesです。
makeLenses ''RoundedRectOpts
Defaultのインスタンスとlensを使用することで、簡便に半径の部分的な指定が可能になります。
例えば右下の角だけ丸くする場合は:
myDiagram :: Diagram B myDiagram = dia1 ||| strutX 2 ||| dia2 where dia1 = fc lightgreen $ getDiaForText "Some very very very very long text" dia2 = fc lightskyblue $ getDiaForText "a" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape w h = roundedRect' w h (with & radiusBR .~ radius) radius = 0.5

withはdefのシノニムに過ぎません。
with :: Default d => d with = def
withを使うことでより自然言語に近づきますので可読性向上に繋がると言えるかもしれません。
ネットのdiagramsの例を見るとこのプラクティスがよく使われると分かります。
これで丸みのある長方形を描くという課題は解決です。
円筒を描く
作図の順番
目標図では、データベースのアイコンは円筒で示されています。
見てきた図形の関数と違って、今回の図形の関数は独自に実装します。 その実装には、軌跡という一つ下の抽象層を使います。
軌跡(Trail)というのは連続に繋いでいるセグメントのリストのようなものです。 セグメントは直線またはベジェ曲線の形を取れます。
軌跡という概念を使って線を伸ばす形で図形をたどります。
まずは、原点と道順を決める必要がありますが、今回は次のように決めます:

1〜6という順で進み、X,Yと記されている頂点はXのステップもYのステップも訪れるということを意味しています。
半楕円
よく見れば円筒の上部が楕円になっているのと、 最下の線が半楕円の形をしているのに気づくことが出来ます。
下の半楕円と上の楕円との半径は同じです。
これを活かして、軌跡の描き方を多少簡略化します。
まず、楕円の描き方をおさらいします:
myDiagram :: Diagram B myDiagram = strokeLoop ell where ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height) width = height * 1.7 height = 3

explodeTrailを使って、この楕円を4つに分けます。
explodeTrailはTrailLikeというtypeclassのインスタンスの型を持っている引数を受けますがこの楕円もTrailLikeの
インスタンスの型を持っているのです。
なぜなら楕円を軌跡の一種として見なすからです。
explodeTrailのアウトプットは楕円を構成する弧のリストです:
myDiagram :: Diagram B myDiagram = ellipseXY (0.5 * width) (0.25 * height) # explodeTrail -- generate a list of diagrams # zipWith lc [green, orange, red, blue] # mconcat where width = height * 1.7 height = 3

explodeTrailは楕円を受けて四分の一のリストを返します。
そして、四分の一ごとに色をつけてから、全ての四分の一をMonoidのmconcatで一つの
図に載せます。
四分の一のリストから二つだけを取ることで半楕円を抽出することが出来ます。
myDiagram :: Diagram B myDiagram = strokeLine halfEll where (halfEll, _sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height) width = height * 1.7 height = 3
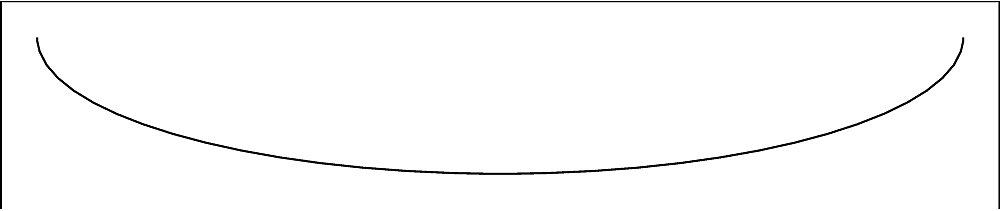
分割後四分の一のリストが戻ります。
そのリストから1つ目と2つ目を1つのリストに、3つ目と4つ目をもう1つのリストに入れます。
リストごとのアイテムをmconcatで組み合せて上半楕円と下半楕円を手に入れます。
ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell
「半楕円」図には一つの半分だけを表示されているのは、どの半分が上、どの半分が下かを突き止めるためだったのです。
直線
楕円以外にも、上下の楕円を繋ぐ、二つの縦の線を描く必要があります。
直線を描く方法は数多くありますがこの場合はfromOffsetsを使います。
fromOffsetsで一直線はもちろん、折れ線を描けます。
fromOffsets :: TrailLike t => [Vn t] -> t
オフセットのリストの引数を受けて軌跡系(TrailLike type classのインスタンス)を戻します。
オフセットを表現するにはベクターを使います。
ベクターの作りには色々な方法があります。
もっとも直接であるのはdata constructorを使用すること:V2 Int Int。
他には、それほど直接でないがより汎用の方法は(特定の次元・タイプに限っていない)
^&という演算子を使うこと:
(^&) :: PrevDim c -> FinalCoord c -> c
Hackageに載っている例から分かるようにベクターまたはポイント、そして、どの次元でも表現出来ます。
2 ^& 3 :: P2 3 ^& 5 ^& 6 :: V3
fromOffsetsと^&を使って、次のように折れ線を表現出来ます。
myDiagram :: Diagram B myDiagram = fromOffsets [ 0 ^& 0 , 1 ^& 0 , 1 ^& 1 ]
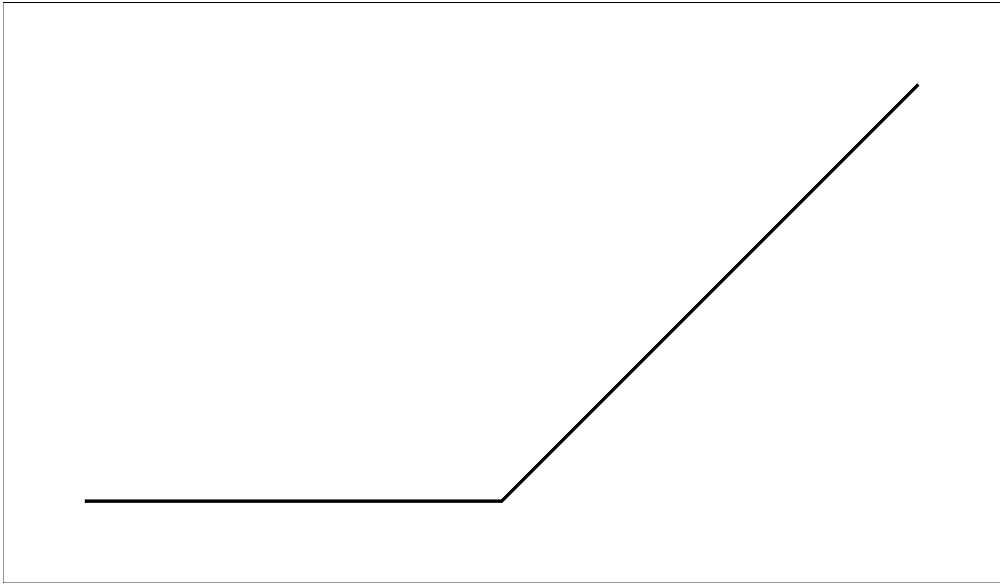
オフセットごとの終点はその次のオフセットの原点となることに気づきます。
まとめて
データベース・アイコンを描くことに必要な要素を揃いました。 上図の順番に円筒を描きます:
- 下半円等(左から右)
- 縦の線(上行)
- 円筒(原終点同一)
- 半円等(描く点の移動のため)
- 縦の線(下行)
myDiagram :: Diagram B myDiagram = centerXY $ strokeLoop $ closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll] where vertBar = fromOffsets [0 ^& height] (halfEll, sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height) width = height * 1.7 height = 3

where節に定義されているものは記事に紹介した要素のみを使っています。
主部式には要素を順番に組み合わせる表現があります。
strokeLoop $ closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll]
Monoidインスタンスを使って連結します。(各図の原点が被るように図が重ね合わせられます)
半楕円のhalfEllと始めて、上に行く縦の線のvertBar、楕円のell、そして最後に
もう一つの半楕円sndHalfEllで完結します。
と言っても、上記のリストの項5の下行の縦の線はどうなったでしょうか?
それはcloseLineで対応しているのです。自動的に現点と原点を繋いで、
軌跡をループにしてくれます。
最後に、軌跡を表示出来る図に変換するのが最後の関数呼び出し、strokeLoopです。
円筒 + テキスト
これで図形が出来ました。次はテキストと一緒に表示してみましょう。
それには記事の冒頭で使ったtextShapeSimpleに、円筒を描く関数を渡す必要がありますが、まず
縦・横を抽象化して引数にします。
cylinder :: Double -> Double -> Diagram B cylinder width height = strokeLoop $ closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll] where vertBar = fromOffsets [0 ^& height] (halfEll, sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height) width = height * 1.7 height = 3
図形でテキストを囲む関数に関しては第一弾では次のような例がありました (テキストだけを変更した):
myDiagram :: Diagram B myDiagram = dia2 where dia2 = fc lightskyblue $ getDiaForText "DB" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape w h = rect w h radius = 0.5

それではrectに変わって今回実装したcylinderを使うとどうなるでしょうか?
myDiagram :: Diagram B myDiagram = dia2 where dia2 = fc lightskyblue $ getDiaForText "DB" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape = cylinder cylinder :: Double -> Double -> Diagram B cylinder width height = strokeLoop . closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll] where vertBar = fromOffsets [0 ^& height] (halfEll, sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height)

cylinderと違ってrectなど第一弾で使った図形を描く関数は 原点を図形の中央に設定したため、テキストが中央に表示されました。
一方、cylinderの実装では原点を指定しなかったため、軌跡を描き始めた原点がテキストの中央に設定されて、テキストも原点を中心に表示されました。
第一弾でも説明した通り、DiagramのMonoidインスタンスで組み合わせたら各図の原点が
被るように図が重ね合わせられるという実装になっているのです。
diagramsは原点を変更するための複数の関数を提供しています。
その一つ、centerXYを使ってみましょう。cylinderの主部式に適用します。
myDiagram :: Diagram B myDiagram = dia2 where dia2 = fc lightskyblue $ getDiaForText "DB" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape = cylinder cylinder :: Double -> Double -> Diagram B cylinder width height = centerXY . strokeLoop . closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll] where vertBar = fromOffsets [0 ^& height] (halfEll, sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height)

今回は円筒の図の原点はcenterXYの名前どおりに縦・横軸の中央に置かれています。
だからといって、一番見た目のいい位置だというわけではありません。
個人的にはテキストをもうちょっと下げる方が見栄えが良いのではないかと思います。
こういう原点の調整は簡単に出来ます。例えばdiagramsが提供しているmoveOriginBy
を使うことで:
-- Move the local origin by a relative vector. moveOriginBy :: (V t ~ v, N t ~ n, HasOrigin t) => v n -> t -> t
cylinderの主部式に、centerXYの適用後、moveOriginByを適用して調整します:
myDiagram :: Diagram B myDiagram = dia2 where dia2 = fc lightskyblue $ getDiaForText "DB" getDiaForText = textShapeSimple mkShape 3 2 . text mkShape = cylinder cylinder :: Double -> Double -> Diagram B cylinder width height = moveOriginBy (0 ^& (-0.25)) . centerXY . strokeLoop . closeLine $ mconcat [halfEll, vertBar, ell, sndHalfEll] where vertBar = fromOffsets [0 ^& height] (halfEll, sndHalfEll) = ellHalves ellHalves :: (Trail' Line V2 Double, Trail' Line V2 Double) ellHalves = ((both %~ mconcat) . (drop 2 &&& take 2)) . explodeTrail $ ell ell :: (Transformable t, TrailLike t, V t ~ V2, N t ~ Double) => t ell = ellipseXY (0.5 * width) (0.25 * height)

表示されている結果は前の図と大きくは変わりませんが、テキストの位置が少し下がってバランスが良くなったと思います。
次回予告
目標図に至るまではまだまだ残っています。
diagramsのタイプの組み合わせ(Monoidインスタンス)のより詳しい説明- 複数のノードを、位置情報をもとに一つの図に結合する
- 矢印とそのラベルを作る関数
まとめ
この第二弾にも目標図に向けての一歩になったと思いますがどうでしたか?
長方形の角に丸みをつけることから初めてdiagramsでの、lensが提供しているインターフェースの
使い方の一つを見ました。
それから、今までのdiagramsの図形を描く関数と違って、
円筒の図の関数cylinderを自分達で実装を試みて、
図形を描く関数の実装に挑みました。
それの下準備として作図順番を決めて、上部・下部として楕円とその半分を使えることに気づきました。
その楕円の半分を手にれるのに軌跡を分割するexplodeTrailに触れてみました。
更に、fromOffsetsを使って手軽な直線からなる折れ線の軌跡を描く方法を使ってみました。
最後にすべてをまとめてcylinderの実装を完成させて、テキストと組み合わせられるように、
原点の調整の関数を二つ、真ん中に設定するものと、相対的に調整するものを使ってみました。
次回も、目標図の完成に向けて、次回予告の一覧から項目を取り上げて、その中心とした記事で進みたいと思います。
採用情報
朝日ネットでは新卒採用・キャリア採用を行っております。


